As lesson 3-2 rate of change and slope takes center stage, this opening passage beckons readers into a world crafted with knowledge, ensuring a reading experience that is both absorbing and distinctly original. The concept of rate of change, a fundamental pillar in understanding functions, will be explored with clarity and precision.
Delving into its practical applications, we will uncover how rate of change and slope empower us to analyze linear functions and make informed predictions.
Prepare to embark on an intellectual journey that unravels the intricacies of rate of change and slope, equipping you with a deeper comprehension of the mathematical landscape.
Understanding Rate of Change: Lesson 3-2 Rate Of Change And Slope
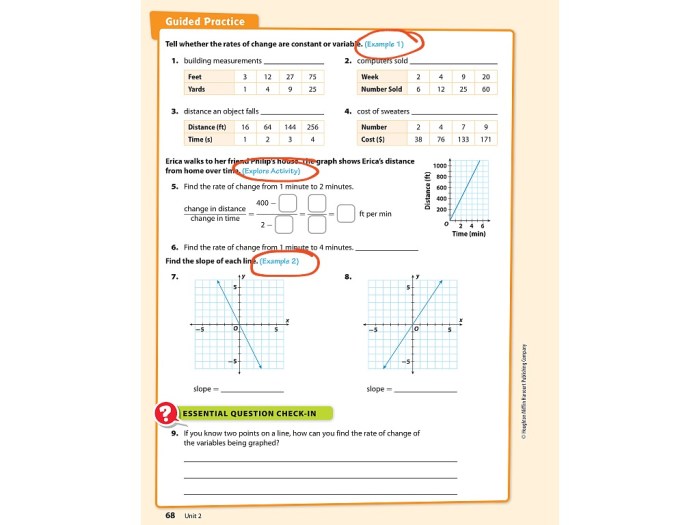
In mathematics, the rate of change refers to the change in the value of a function with respect to the change in its input. It measures the steepness of the function’s graph and can be used to describe how quickly a quantity is increasing or decreasing.
For example, if the function represents the height of a growing plant over time, the rate of change would indicate how fast the plant is growing in terms of height per unit time.
Methods for Calculating Rate of Change
There are several methods for calculating the rate of change of a function:
- Graphical Method:Draw the graph of the function and determine the slope of the tangent line at a given point.
- Formula Method:Use the formula for the derivative of the function, which provides the instantaneous rate of change at any point.
- Difference Quotient:Calculate the average rate of change over an interval using the formula: “` Average Rate of Change = (Change in Output) / (Change in Input) “`
Slope as a Measure of Rate of Change
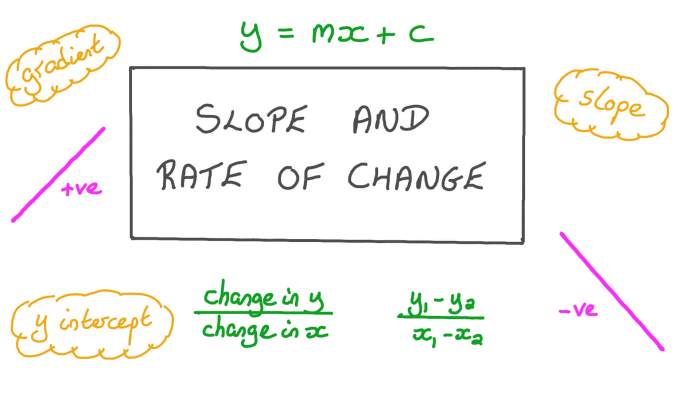
The slope of a line is a measure of its steepness. It is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate as you move along the line.
Slope can be used to determine the rate of change of a linear function. For example, if a line has a slope of 2, then the y-coordinate increases by 2 units for every 1 unit increase in the x-coordinate.
Steepness of a Line
The slope of a line determines its steepness. A line with a positive slope is increasing, while a line with a negative slope is decreasing. The steeper the line, the greater the rate of change.
Analyzing Linear Functions, Lesson 3-2 rate of change and slope
Slope can be used to analyze linear functions. For example, the slope of a line can be used to determine the following:
- The rate of change of the function
- The y-intercept of the function
- The equation of the function
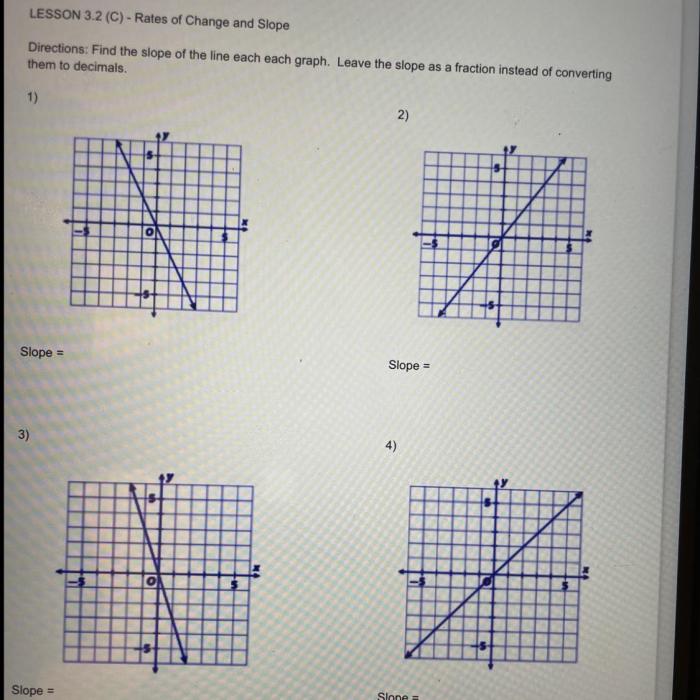
Calculating Slope
Slope is a numerical measure that describes the steepness of a line. It is calculated by dividing the change in the vertical axis (y-axis) by the change in the horizontal axis (x-axis).
The formula for calculating slope is:
$$m = \fracy_2
- y_1x_2
- x_1$$
where:
- $m$ is the slope
- $y_1$ and $y_2$ are the y-coordinates of two points on the line
- $x_1$ and $x_2$ are the x-coordinates of two points on the line
The slope can be calculated using different methods, such as the two-point method and the slope-intercept form.
Two-Point Method
The two-point method is a simple method for calculating the slope of a line. It involves using two points on the line and plugging their coordinates into the slope formula.
For example, if we have two points on a line, $(2, 3)$ and $(4, 7)$, the slope can be calculated as follows:
$$m = \fracy_2
- y_1x_2
- x_1$$
$$m = \frac7
- 34
- 2$$
$$m = 2$$
Therefore, the slope of the line is 2.
Slope-Intercept Form
The slope-intercept form is another method for calculating the slope of a line. It involves converting the equation of the line into the form y = mx + b, where m is the slope and b is the y-intercept.
For example, if we have the equation of a line, y = 2x + 1, the slope can be calculated by identifying the coefficient of x, which is 2.
Therefore, the slope of the line is 2.
Importance of Using Correct Units
It is important to use the correct units when calculating slope. The slope represents the ratio of the change in the vertical axis to the change in the horizontal axis, so the units of the slope will depend on the units of the axes.
For example, if the vertical axis is measured in meters and the horizontal axis is measured in seconds, the slope will have units of meters per second.
Applications of Rate of Change and Slope
Rate of change and slope find widespread applications across various fields, including physics, economics, and biology. They provide valuable insights into the behavior of systems and enable researchers to make predictions and draw conclusions based on observed data.
Physics
- Velocity and Acceleration:Slope of a position-time graph represents velocity, while the slope of a velocity-time graph represents acceleration.
- Force and Displacement:Slope of a force-displacement graph represents the spring constant, a measure of the stiffness of a spring.
- Electrical Circuits:Slope of a voltage-current graph represents the resistance of a resistor.
Economics
- Demand and Supply:Slope of a demand or supply curve indicates the responsiveness of quantity demanded or supplied to changes in price.
- Marginal Cost and Revenue:Slope of a marginal cost or revenue curve represents the change in cost or revenue for each additional unit produced or sold.
li> Interest Rates:Slope of a yield curve depicts the relationship between interest rates and the time to maturity of bonds.
Biology
- Population Growth:Slope of a population growth curve represents the rate of population increase.
- Enzyme Kinetics:Slope of a Michaelis-Menten curve represents the maximum reaction velocity of an enzyme.
- Diffusion:Slope of a concentration-distance graph represents the rate of diffusion.
Limitations of Rate of Change and Slope
While rate of change and slope are powerful tools, it is essential to recognize their limitations:
- Nonlinear Relationships:Rate of change and slope assume a linear relationship between variables, which may not always be the case in real-world scenarios.
- Outliers and Noise:Extreme values or random fluctuations in data can distort the calculated slope and rate of change.
- Correlation vs. Causation:Slope only indicates a correlation between variables, not necessarily a causal relationship.
FAQs
What is the significance of rate of change?
Rate of change measures the rate at which a function’s output changes with respect to its input. It provides valuable insights into the behavior and dynamics of functions.
How is slope related to rate of change?
Slope is a numerical measure of the steepness of a line and is directly related to the rate of change of a linear function. A positive slope indicates an increasing function, while a negative slope indicates a decreasing function.
What are the practical applications of rate of change and slope?
Rate of change and slope find applications in diverse fields such as physics, economics, and biology. They are used to analyze motion, predict growth patterns, and model real-world phenomena.